Fun with temperature charts IITheir standard chart of the average global temperature since 1979 is here: http://www.drroyspencer.com/latest-global-temperatures and the data is here: http://vortex.nsstc.uah.edu/data/msu/t2lt/uahncdc.lt The complete dataset includes subsets of the globe like the north and south polar regions and the 48 contiguous U.S. states. I've always wanted to make charts of other regions and using models other than the standard chart's 13 month rolling average. I already have some temperature charting code here: http://www.heurtley.com/richard/tchart and it was easy to adapt it to the new dataset. The results are here:
The dataset from the vortex.nsstc.uah.edu web server must first be saved as a text file. The program reads the input text file in a flexible manner. The first two columns must be year and month but the remaining columns are not fixed. A column entitled "Land" is assumed to be a subset of the preceeding column and a column entitled "Ocean" is assumed to be a subset of the twice-preceeding column. The program has three modeling functions:
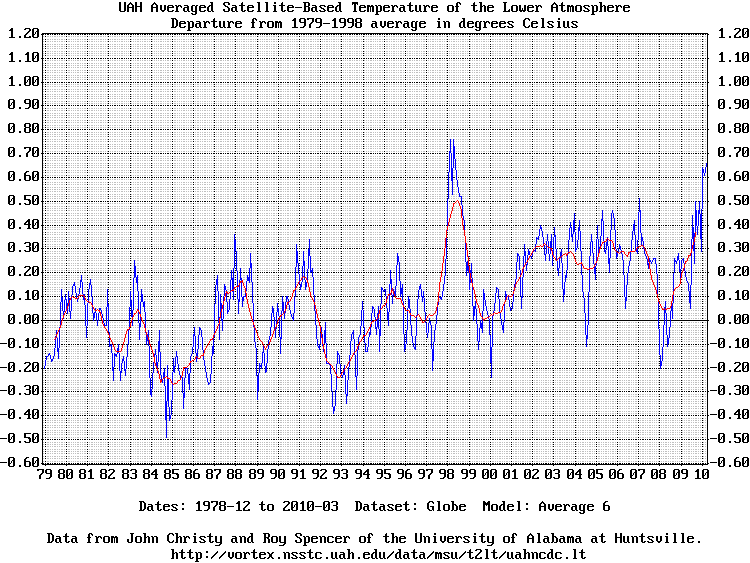
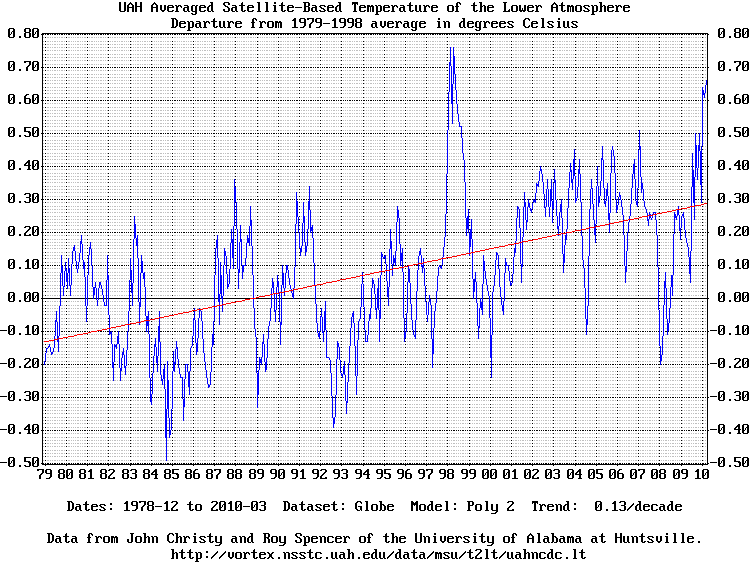
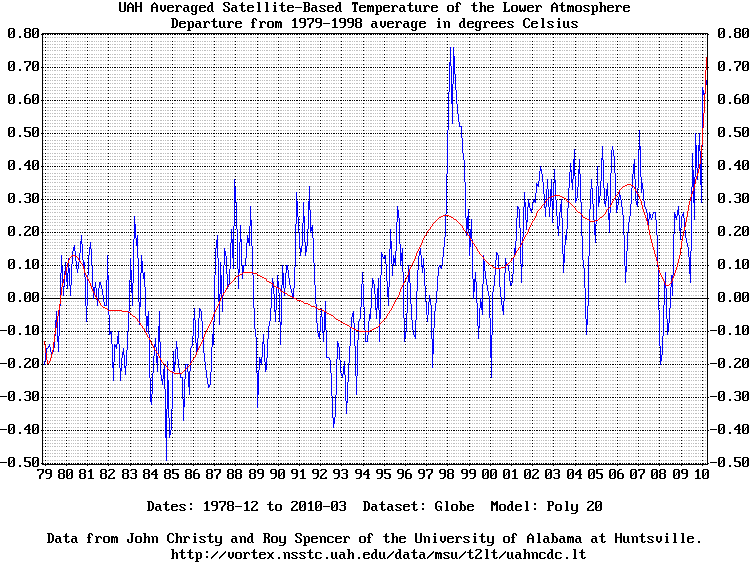
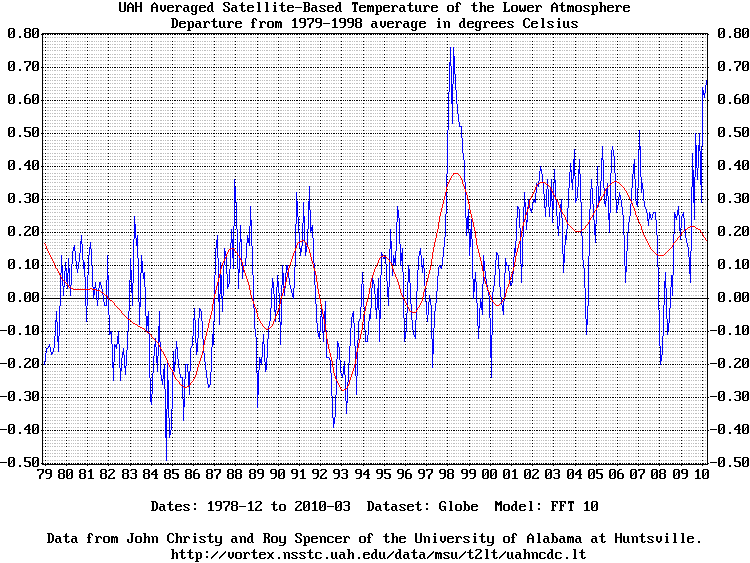
The rolling average model averages each point and the N points surrounding it in both directions. The standard chart uses a 13 point rolling average which is specified in this program as "-ave 6" because 6+1+6 = 13. The polynomial model calculates a least-square error best-fit polynomial curve. N is the number of terms. A value of one calculates the average temperature. A value of two calculates the best-fit straight line. A value of three calculates the best-fit parabola, etc. When the best fit line is calculated the program renders the 10 year temperature trend on the chart. A value of 20 produces nice curves. Values much more than 20 start to show precision effects. The FFT model smooths the data with a low-frequency filter created by calculating the data's Fourier Transform, zeroing the high-frequency terms, and re-calculating the sample values. N is the number of low-frequency terms to retain. A value of one retains the lowest frequency term which is the average of the data. A value of 10 produces nice curves. The FFT is periodic so the ends try to meet and thus deviate from the data. None of these models have any analytic or predictive power whatsoever. This whole exercise is best considered as mathematical artwork. The default resolution is 150dpi which is good for printing charts on standard letter (8.5" by 11") paper. Charts intended for viewing on web sites are best rendered with a lower dpi value. Here are some sample charts rendered at 75dpi (-dpi 75). The dataset is assumed to have been saved as file "temps.txt". Click on a chart to download and render the full-size 150dpi chart.
My version of the original standard chart. The current standard chart has
a low limit of -0.8:
Globe dataset with best-fit straight line (-poly 2) and 10 year trend:
Globe dataset with 20 term polynomial fit (-poly 20):
Globe dataset with FFT low frequency filter (-fft 10):
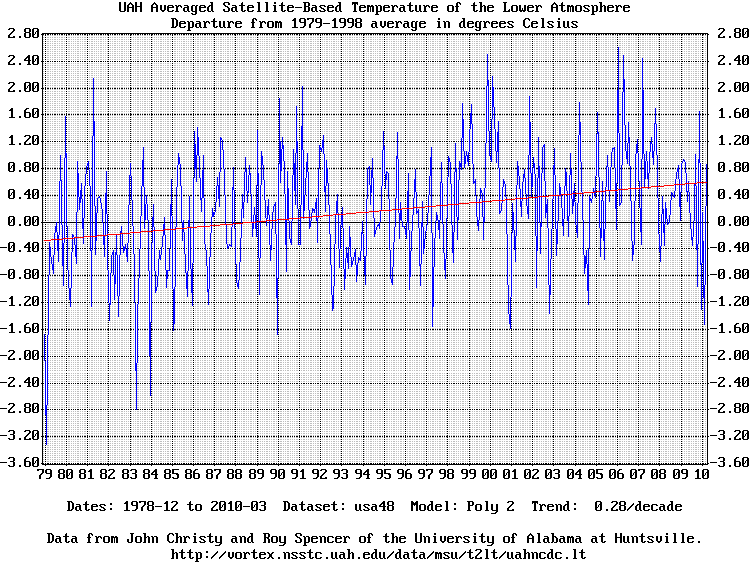
USA48 dataset with best-fit straight line (-poly 2) and 10 year trend:
Copyright © 2010-2011, Richard Heurtley. All rights reserved. |